Problem 11
In triangle \(ABC\) \(I\) is the incenter and \(J\) is the \(B\)-excenter. \(BH\) is height. Reconstruct \(ABC\) given the points \(I,J,H\).
Tags: triangle circles incircle
Solution
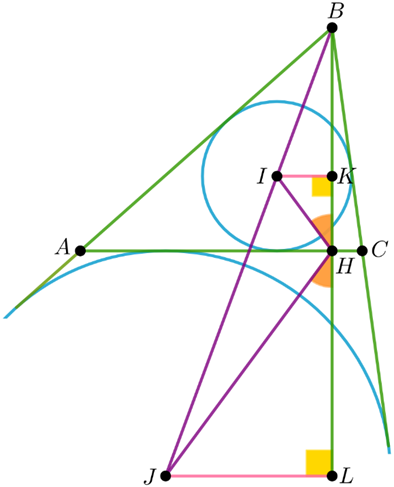
Let \(K\) and \(L\) be he projections of \(I\) and \(J\) respectively on \(BH\). Let the inradius and \(B\)-exradius be \(r\) and \(r_b\) respectively. Note that \(\frac{IK}{J L}=\frac{IB}{J B}=\frac{r}{r_b} =\frac{KH}{HL}\). This means that the triangles \(IKH\) and \(J LH\) are similar and \(\angle IHK=\angle J HL\), i.e. \(AC\) and \(BH\) are the bisectors of \(\angle J\). Hence we get the following construction:
- Draw the internal bisector \(l\) of \(\angle IHJ\);
- Draw the circles with the centers \(I\) and \(J\) touching \(l\);
- Draw their common external tangents and mark the points A and C of their intersections with \(l\) and the point \(B\) of their intersection. The triangle \(ABC\).