Problem 37

Let the side \(AC\) of triangle \(ABC\) touch the incircle and the corresponding excircle at points \(K\) and \(L\) respectively. Let \(P\) be the projection of the incenter onto the perpendicular bisector of \(AC\). It is known that the tangents to the circumcircle of triangle \(BKL\) at \(K\) and \(L\) meet on the circumcircle of \(ABC\). Prove that the lines \(AB\) and \(BC\) touch the circumcircle of triangle \(PKL\).

XV Geometrical Olympiad in Honour of I.F. Sharygin, correspondence round, problem 14

Tags: triangle circles incircle circumcircle

Solution

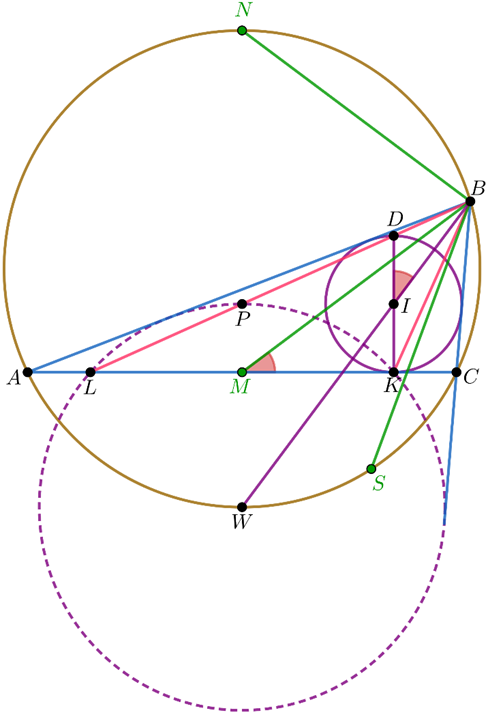
Suppose that \(AB>BC\). Let \(M\) be the midpoint of \(AC\), \(N\) be the midpoint of arc \(ABC\), \(NW\) and \(KD\) be the diameters of the circumcircle and the incircle respectively. By the assumption, the tangents to the circle \(BKL\) at \(K\) and \(L\) meet at \(W\), i.e. \(BW\) is the symedian of triangle \(BKL\). Furthermore \(B,D,L\) are collinear and \(BW\) bisects the segment \(KD\). Hence the triangles \(BKL\) and \(BDK\) are similar, i.e. \(\angle BMC=\angle BID =(\angle C−\angle A)/2\). Then \[\angle BMN = \frac{\pi −\angle C+\angle A}{2}=\angle BNM\] and \(BM=BN\). Let \(S\) be a point on the arc \(AWC\) such that \(\angle SBC=\angle ABM\). Then \[\angle SNB= \angle ABM +\angle BAC=\angle BMC= \angle NSB,\] i.e. \(BS=BN=BM\) (figure 1). By the similarity of the triangles \(ABM\) and \(SBC\) we have \[AB\cdot BC=BM\cdot BS=BM^2=\frac{2AB^2+2BC^2−AC^2}{4}.\] Therefore \(AC^2=2(AB−BC)^2\), or \(AC=\sqrt2KL\). Applying the Stewart theorem to triangle \(AWC\) and cevian \(WK\) we obtain that \[WK^2=WC^2−AK\cdot KC=WI^2−(AM^2−MK^2)=WI^2−MK^2= WI^2−PI^2=WP^2\] (by the trident theorem, \(WC=WI\)). Thus \(P,K,L\) lie on the circle centered at \(W\).

Let \(R,r\) be the circumradius and the inradius of triangle \(ABC\). Then the distance from \(W\) to line \(AB\) is equal to \[BW \sin\frac{\angle B}{2} =2R\cos\frac{\angle C−\angle A}{2}\sin\frac{\angle B}{2} = R(\sin\angle A+\sin\angle C).\] By the Carnot theorem \(R+r=R(\sin\angle A+\sin\angle B+\sin\angle C)\), therefore this distance is equal to \(R(1−\cos\angle B)+r=WM+MP=WP\), which is equivalent to the required assertion.

Note. The triangle which has a side \(\sqrt 2\) times greater than the difference between the other two sides is also considered in A. Akopjan's problem ( V Geometrical Olympiad in Honour of I.F. Sharygin, final round, 9th class, problem 6).