Problem 41

Let us be given a convex quadrilateral \(ABCD\) none of whose diagonals is its axis of symmetry and \(DA+AB=DC+CB\). Let \(N_a\) and \(N_c\) be the Nagel points of \(ABD\) and \(CBD\) respectively. Prove that \(N_aN_c\perp BD\) iff the length of \(BD\) is the quarter of \(ABCD\)'s perimeter.

taken from "The Nagel point and the difference triangle", journal “Quantum”, 2019 №9, pages 32-33

Tags: quadrilateral triangle circles incircle Nagel point

Solution

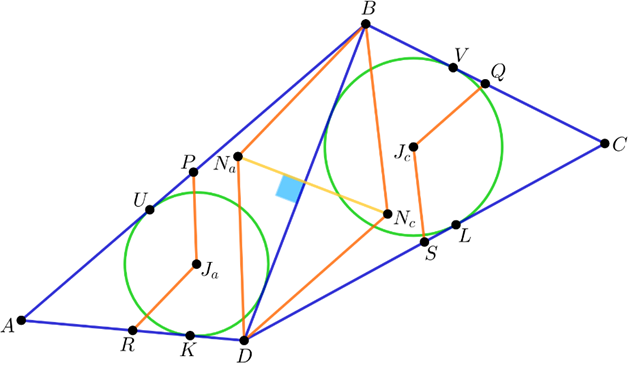
Let \(P, Q, R, S\) be the midpoints of \(AB, BC, CD, DA\) respectively (figure 1). Let \(U\) and \(K\) be the touch-points of the incircle of \(ABD\) with center \(J_a\) and the sengments \(AB\) and \(AD\) respectively. Similarly define \(J_c, V, L\). Clearly \[N_aN_c\perp BD\iff N_aB^2-N_aD^2=N_cB^2-N_cD^2.\] Using the fact that the incenter of the triangle is the Nagel point of its medial triangle the last is equivalent to \begin{align*} J_aR^2-J_aP^2=J_cS^2-J_cQ^2 &\iff (J_aK^2+KR^2)-(J_aU^2+UP^2)=(J_cL^2+LS^2)-(J_cV^2+VQ^2)\\ &\iff KR^2-UP^2=LS^2-VQ^2\\ &\iff (AB-BD)^2-(AD-BD)^2=(CB-BD)^2-(CD-BD)^2\\ \end{align*} \begin{align*} \iff BD &=\frac{AB^2-BC^2+CD^2-DA^2}{2(AB-BC+CD-DA)}\\ &=\frac{(AB+DA)(AB-DA)+(CD+BC)(CD-BC)}{2(AB-BC+CD-DA)}\\ &=\frac{AB+BC+CD+DA}{4}. \end{align*}

Note. In fact \(N_aN_c\) is the perpendicular bisector of \(BD\) in the problem. Also one may show that the bisectors of angles \(N_aBJ_a\) and \(N_cBJ_c\) make an angle of \(45^\circ\).