Problem 49

Let \(I\) be the incenter of the triangle \(ABC\). Let the respective excircle touch the segment \(AC\) at the point \(K\). Let \(W\) be the second point of intersection of \(BI\) and the circumcircle of \(ABC\), and let \(P\) be the reflection of \(I\) in the \(B\)-height of \(ABC\). It is known that \(\angle IKW=90^\circ\). Then find the measure of \(\angle BPK\).

XXIV Kolmogorov Cup, first tour, senior league, problem 6

Tags: triangle circles incircle circumcircle symmedian

Solution

Let \(L\) be the touchpoint of \(AC\) with the incircle. Draw the diameter \(LN\) in the incircle and the altitude \(BH\). Let \(M\) be the midpoint of \(AC\) (figure 1).

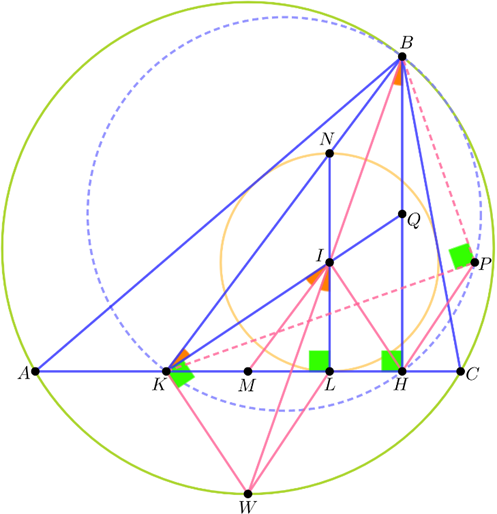
The points \(N\) and \(K\) are corresponding points in the excircle and the incircle so they are collinear with the external homothety center \(B\). \(KN\parallel BH\) so \(KI\) passes through the midpoint \(Q\) of \(BH\). From the conditions \(MK=ML\) and \(\angle IKW=90^\circ\) we get that \(WK\) and \(WL\) touch the circle \(KLI\). By the symmedian theorem \[\angle IBH=\angle WIL=\angle MIK=\angle IKB\] so the triangles \(QIB\) and \(QBK\) are similar. Hence \(QI\cdot QK=QB^2=QH^2\), i.e. the triangles \(QIH\) and \(QHK\) are similar too and \[\angle BPH=\angle BIH=180^\circ - \angle QBI-\angle QHI=180^\circ - \angle BKH.\] Consequently \(B, P, H, K\) are concyclic and \(\angle BPK=\angle BHK=90^\circ\).