Problem 5

The points \(D\) and \(E\) on the side \(AC\) of the triangle \(ABC\) are chosen so that the incircles of \(ABD\) and \(CBE\) with respective centers \(J_a\) and \(K_c\) have equal radii. Also \(J_c\) and \(K_a\) are the incenters of \(CBD\) and \(ABE\) respectively. Prove that the circles \(BJ_aJ_c\) and \(BK_aK_c\) concur second time on the bisector of angle \(B\).

XXIV Kolmogorov Cup, individual olympiad, senior group, conclusion, problem 7

Note. In fact this problem occurred in the olympiad in generalized form for circumscribed quadrilaterals by I. Bogdanov and I. Frolov.

Tags: triangle circles incircle

Solution

First let's prove the following lemma.

Lemma. The points \(D\) and \(E\) are chosen on the side \(AC\) of the triangle \(ABC\). Then the second common external tangents (different than \(AC\)) to the pairs of incircles of \(ABD\) and \(CBE\), \(ABE\) and \(CBD\) concur on the extension of \(AC\) or are parallel.

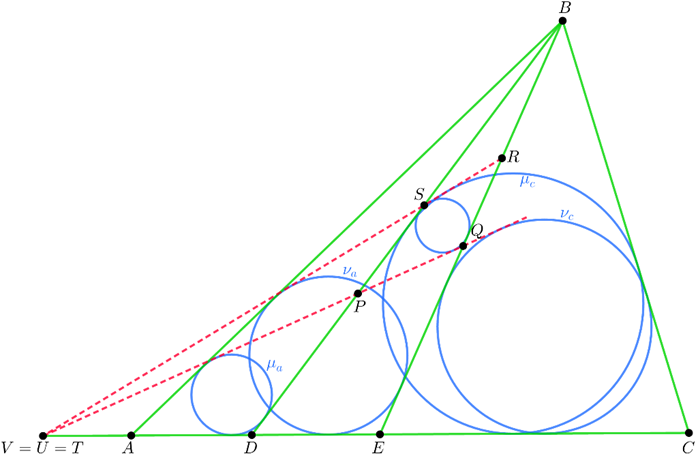
Proof. Denote by \(\mu_a, \mu_c, \nu_a, \nu_c\) the incircles of \(ABD, CBD, ABE, CBE\) respectively (figure 1). Let \(U\) be the external homothety center of \(\mu_a\) and \(\nu_c\), and \(T\) be that of \(\mu_c\) and \(\nu_a\). Suppose for the sake of contradiction that \(U\ne T\). Assume that the \(T, U, A, C\) succeed in this order. Let the second common external tangent of \(\mu_a\) and \(\nu_c\) intersect \(BD\) and \(BE\) in \(P\) and \(Q\) respectively. Similarly define \(S\) and \(R\). We have \[\begin{cases} UP+PB=UA+AB \\ TA+AB=TR+RB \\ UQ-QB=UC-CB \\ TS-SB=TC-CB \end{cases}.\] Subtracting the first two equations and the last two ones we get \[\begin{cases} AB+BC-CA=SR+RB+BS \\ AB+BC-CA=PB+BQ-QP \end{cases}.\] Hence \(PS+RQ=RS+PQ\) and \(PQRS\) is circumscribed quadrilateral. Let the lines \(SR\) and \(PQ\) intersect at \(V\). We have \[\begin{cases} VS-SB=VQ-QB \\ UQ-QB=UC-CB \\ TS-SB=TC-CB \end{cases}.\] Subtracting the last two equations we get \(TS-SB-UQ+QB=TU\). But according to the first equation \(VU-VT=TS-SB-UQ+QB=TU\) which is impossible due to the triangle inequality: \(VU-VT< TU\). Thus \(V\equiv U\equiv T\). The case when one of the points \(U\) or \(T\) does not exist (i.e. is at infinity) follows by a limit argument.

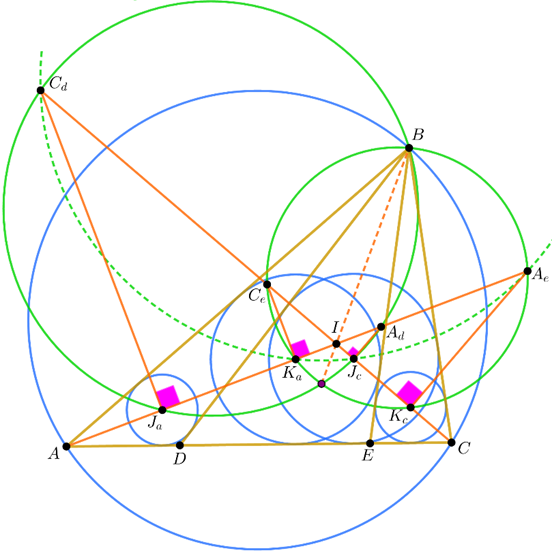
Back to our problem. Let the \(A\)-bisector intersect the circles \(BJ_aJ_c\) and \(BK_aK_c\) at the points \(A_d\) and \(A_e\) other than \(J_a\) and \(K_a\) respectively. Similarly define \(C_d\) and \(C_e\) (figure 2). Note that \[\angle J_aC_dJ_c=\angle J_aBJ_c=\frac{\angle B}{2}=90^\circ- \angle C_dIJ_a\] so \(A_dC_d\) is diameter. Similarly \(A_eC_e\) is diameter too. According to the lemma \(J_aK_c\parallel AC\parallel J_cK_a\) and moreover \(\angle C_dJ_aI=90^\circ=\angle A_eK_cI\) so the triangles \(J_aC_dI\) and \(A_eK_cI\) are similar. Hence \[\frac{C_dI}{A_eI}=\frac{J_aI}{K_cI}=\frac{K_aI}{J_cI}\] and the triangles \(C_dIK_a\) and \(A_eIJ_c\) are similar too. This means that \(\angle K_aC_dI= \angle J_cA_eI\) and \(A_e, C_d, K_a, J_c\) are concyclic. It remains to note that \(I\) is the radical center of the circles \(BJ_aJ_c, BK_aK_c\) and \(A_eC_dK_aJ_c\) therefore the first two circles concur on \(BI\) second time.