Problem 66

Let us be given an isosceles tetrahedron \(ABCD\), i.e. it has equal opposite edges. Choose a point \(X\) on its circumsphere \(\Omega\) different from the points \(A, B, C, D\). Prove that the center of the sphere passing through the reflections of \(X\) in the faces of \(ABCD\) lies on \(\Omega\).

XXIII Kolmogorov Cup, second tour, senior league, problem 1

Tags: 3D tetrahedron isosceles tetrahedron spheres circumsphere isogonals

Solution

First let's prove that for an arbitrary tetrahedron \(ABCD\) and arbitrary point \(P\) in space not lying in the face-planes of \(ABCD\) exists the isogonal conjugate of \(P\) with respect to \(ABCD\), that is a point \(Q\) such that for any edge \(e\) of \(ABCD\) the planes \(Pe\) and \(Qe\) are symmetric with respect to the bisector plane of the dihedron at edge \(e\).

Let \(P_A, P_B, P_C, P_D\) be the reflections of \(P\) in respective faces of \(ABCD\). Since \(DP_A=DP_B=DP_C\) we deduce that the perpendicular line to \(P_AP_BP_C\) through \(D\) passes through the circumcenter \(Q\) of \(P_AP_BP_CP_D\). The other three lines through \(A, B, C\) defined similarly pass through \(Q\) too.

Now let's show that, for example, the planes \(ABP\) and \(ABQ\) are symmetric wrt the bisector plane of dihedron \(AB\). Indeed, \[\angle(ABP, ABQ) = \frac{\angle(ABP, ABP_C)}2 = \frac{\angle(ABP_D, ABP_C) - \angle(ABP_D, ABP)}2 = \angle(ABP_D, ABQ) - \angle(ABP_D, ABC) = \angle(ABC, ABQ).\]

Back to our problem. Now it is equivalent to the following theorem:

Theorem. The isogonal conjugate of any point \(X\) on the circumsphere \(\Omega\) of the isosceles tetrahedron \(ABCD\) lies on \(\Omega\), that is the circumsphere of isosceles tetrahedron is invariant wrt isogonal conjugacy.

Proof. Let \(O\) be the center of \(\Omega\). Let \(Y\) be the second point of intersection of \(\Omega\) and the line through \(D\) passing through the isogonal conjugate of \(X\). The points \(X\) and \(Y\) lie in isogonal planes wrt each of the dihedrons \(DA, DB, DC\). We need to show that these points lie in isogonal planes wrt each of the dihedrons \(AB, BC, CA\) too.

Note that the circumcenter and the incenter of \(ABCD\) coincide. Indeed, since the opposite edges of \(ABCD\) are equal we get that its faces are equal triangles. The locus of points \(Z\in \Omega\) such that \(\angle AZB=\angle ACB\) is the union of two circular arcs which are symmetric wrt the plane \(ABO\). This means that the planes \(ADB\) and \(ACB\) are symmetric wrt \(ABO\) for \(\angle ADB=\angle ACB\). So \(O\) lies on the bisector plane of the dihedron \(AB\). Similarly \(O\) lies on the bisector planes of the other dihedrons and thus coincides with the incenter.

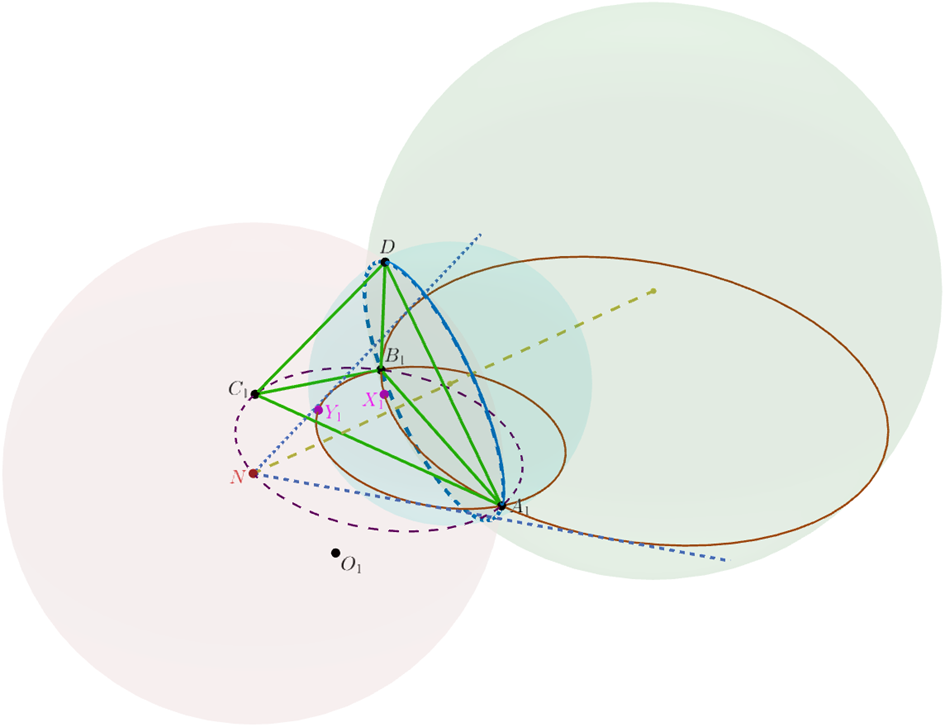
Invert with center \(D\) (figure 1). Denote by \(Z_1\) the image of any point \(Z\). In force of the equality of the faces of \(ABCD\) we get \(\angle BA_1D= \angle ABD= \angle ACD = \angle C_1A_1D\) and so on.

Clearly \(A_1, B_1, C_1, X_1, Y_1\) are coplanar. Taking into account the equality \(\angle B_1A_1D=\angle C_1A_1D\) and the two other similar ones, as well as the fact that \(X_1\) and \(Y_1\) lie in isogonal planes wrt the dihedrons \(DA_1, DB_1, DC_1\) we deduce that \(X_1\) and \(Y_1\) are isogonal conjugates wrt \(A_1B_1C_1\).

It's not hard to check that \(O_1\) is the reflection of \(D\) in \(A_1B_1C_1\). Angles between spheres are preserved under inversion so since the plane \(ABO\) makes equal angles with \(ABD\) and \(ABC\), the sphere \(A_1B_1O_1D\) makes equal angles with the plane \(A_1B_1D\) and the sphere \(A_1B_1C_1D\). This is possible only in the case when the circumcenter \(N\) of \(A_1B_1O_1D\) lies on the sphere \(A_1B_1C_1D\). The tetrahedron \(A_1B_1O_1D\) is symmetric wrt the plane \(A_1B_1C_1\) so \(N\) lies on the circle \(A_1B_1C_1\). Furthermore \(NA_1=NB_1\) therefore \(N\) is the midpoint of the arc \(A_1C_1B_1\).

It's not hard to check that since \(X_1\) and \(Y_1\) are isogonal conjugates wrt \(A_1B_1C_1\), the circles \(A_1B_1X_1\) and \(A_1B_1Y_1\) make equal angles with the circle centered at \(N\) and passing through \(A_1\) and \(B_1\). This means that \(N\) is the external homothety center of the circles \(A_1B_1X_1\) and \(A_1B_1Y_1\). \(NA_1=NB_1=NC_1\) so the line passing through the circumcenters of \(A_1B_1DX_1\) and \(A_1B_1DY_1\) passes through \(N\) too. This and the previous judgements lead to the conclusion that \(N\) is the external homothety center of the spheres \(A_1B_1DX_1\) and \(A_1B_1DY_1\) too. Therefore the sphere \(A_1B_1O_1D\) with center \(N\) passing through \(A_1\) makes equal angles with the spheres \(A_1B_1DX_1\) and \(A_1B_1DY_1\), so its preimage plane \(ABO\) also makes equal angles with the planes \(ABX\) and \(ABY\). Similarly the planes \(BCO\) and \(CAO\) make equal angles with the pairs of the planes \(BCX, BCY\) and \(CAX, CAY\) whence the conclusion follows.