Problem 72
Let the sphere \(\omega\) with center \(I\) be inscribed in a
- hexahedron which has only quadriangular faces and in each vertex of which exactly three faces meet;
- dodecahedron which has only pentagonal faces and in each vertex of which exactly three faces meet.
XXIV Kolmogorov Cup, third tour, senior league, problem 8
Note. In fact this problem occurred in the olympiad in simplified form by I. Frolov.
Tags: 3D dodecahedron hexahedron spheres insphere isogonals conics
Solution
First let's prove the following two lemmas which are vital parts of the solution.
Lemma 1. Let us be given a polygon and a point \(P\) in its plane. Then if the projections of \(P\) on the sidelines of the polygon are concyclic, there exists an isogonally conjugate point of \(P\) wrt the polygon.
Proof. Let \(A, B, C\) be three consecutive vertices of the polygon and let \(P_1, P_2\) be the projections of \(P\) on \(AB, BC\) respectively. Let \(P_1, P_2\) be mapped to \(P_1', P_2'\) under the homothety with center \(P\) and coefficient \(2\), and let the circumcenter of the pedal polygon of \(P\) be mapped to \(Q\).
\(P_1'B=PB=P_2'B\) so \(B\) lies on the perpendicular bisector of \(P_1'P_2'\). On the other hand the circle with center \(Q\) passes through \(P_1', P_2'\) so \(Q\) lies on the perpendicular bisector of \(P_1'P_2'\). Hence \(BQ\perp P_1'P_2'\parallel P_1P_2\) which means that \(P\) and \(Q\) lie on isogonals in angle \(B\). Similarly \(P\) and \(Q\) lie on isogonals wrt other angles of the polyhedron and thus are isogonally conjugate.
Lemma 2. If a sphere \(\gamma\) with center \(I\) touches a polygon in an internal point and moreover the projections of \(I\) on the sidelines of the polygon are concyclic then the second tangent planes to \(\gamma\) through the sides of the polygon are concurrent.
Proof Let \(P\) be the projection of \(I\) on the polygon. The projections of \(P\) and \(I\) on the sidelines of the polygon coincide therefore lemma 1 yields the existence of isogonally conjugate to \(P\) point \(Q\). According to the isogonal property of conics there exists an ellipse \(\varepsilon\) with foci \(P, Q\) inscribed in the polygon.
Consider the hyperbola with foci being the endpoints of the major axis of \(\varepsilon\) passing through \(P\) and \(Q\) which is in a plane perpendicular to the one of the polygon. Particularly consider the branch of this hyperbola passing through \(Q\). It's not hard to check that this hyperbola is the locus of the cone vertices passing through \(\varepsilon\) (which have circular sections perpendicular to their axes). Moreover these cones have their inspheres and exspheres touching the base at \(P\) and \(Q\). Since each point of the hyperbola corresponds to a unique insphere and exsphere and vice versa, \(\gamma\) corresponds to a unique point \(S\) of the hyperbola. The cone \(S\varepsilon\) touches \(\gamma\) so the side planes of the pyramid with vertex \(S\) and the given polygon in its base touch the cone and \(\gamma\) as needed.
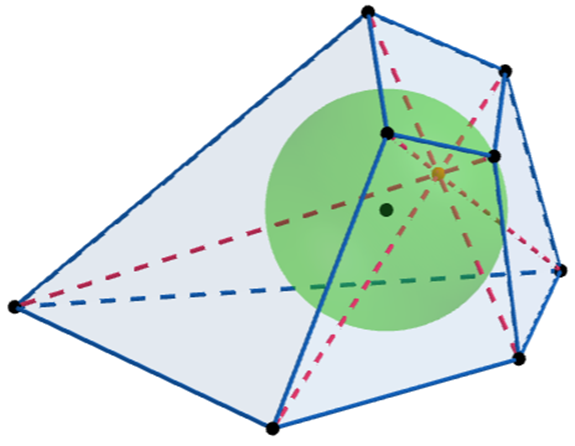
Done with lemmas. Consider the hexahedron case (figure 1). Let \(ABCDA_1B_1C_1D_1\) be the hexahedron so that \(ABCD\) is a face and \(X\) and \(X_1\) are opposite vertices for each \(X\in \{A, B, C, D\}\). Denote by \(l_1, l_2, l_3\) the lines joining the touch-points of \(\omega\) with opposite faces.
According to lemma 2 the extensions of the faces \(ABD_1C_1, BCA_1D_1, CDB_1A_1, DAC_1B_1\) are concurrent in a point \(S\). Thus the touch-points of these faces with \(\omega\) are coplanar. Hence the pair of lines among \(l_1, l_2, l_3\) corresponding to these faces, say \(l_1, l_2\), is concurrent. Similarly the other two pairs are concurrent too whence all three \(l_1, l_2, l_3\) are concurrent in a point \(P\) (since these lines are not coplanar).
Consider the section of the quadrihedron with vertex \(S\) by the plane through \(l_1, l_2\). Clearly it is a circumscribed quadrilateral. It is well-known that its diagonals are concurrent in the point of intersection of the lines joining the touch-points of opposite sides with the incircle, i.e. in \(P\). Hence \(P\) lies in the plane \(ACA_1C_1\). Similarly \(P\) lies in the planes \(ABA_1B_1\) and \(BCB_1C_1\). Hence \(P\) is the intersection point of these three planes and all the diagonals of the hexahedron pass through it.
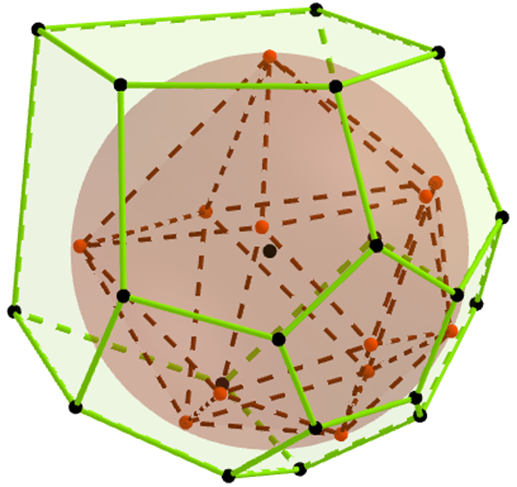
Now proceed to the dodecahedron case. Let \(A, B, C, D, E, F, A_1, B_1, C_1, D_1, E_1, F_1\) be the touch-points of the faces with \(\omega\) so that \(X\) and \(X_1\) lie in opposite faces for each \(X\in\{A, B, C, D, E, F\}\), the points \(A, B, C, D, E\) (in this order) lie in the adjacent faces of \(F\).
Denote by \(\mathcal Q\) the icosahedron (dual to the dodecahedron) having these \(12\) touch-points as its vertices (figure 2). Let \(f\) be a face of the dodecahedron. Denote by \(T_1, T_2, T_3, T_4, T_5\) the touch-points of \(\omega\) with the faces adjacent to \(f\). According to lemma 2 the extensions of these five faces are concurrent in a point \(S\) through \(T_i, i\in[5]\). This means that \(T_1, T_2, T_3, T_4, T_5\) lie on the tangent circle of \(\omega\) and the cone with vertex \(S\). Hence \(\mathcal Q\) has the property that for any of its vertices its five adjacent vertices are concyclic.
Invert with center \(F_1\). Denote by \(X'\) the image of \(X\). Under this inversion all the vertices of \(\mathcal Q\) except for \(F_1\) are sent to the plane \(\omega'\). The circles \(F_1A_1DEC_1\), \(F_1B_1EAD_1\), \(F_1C_1ABE_1\), \(F_1D_1BCA_1\), \(F_1E_1CDB_1\) become the lines \(A_1'D'E'C_1'\), \(B_1'E'A'D_1'\), \(C_1'A'B'E_1'\), \(D_1'B'C'A_1'\), \(E_1'C'D'B_1'\) which make the pentagon \(A'B'C'D'E'\) and the inscribed star \(A_1'B_1'C_1'D_1'E_1'\). Furthermore the quadrilaterals \(A'D_1'E_1'C'\), \(B'E_1'A_1'D'\), \(C'A_1'B_1'E'\), \(D'B_1'C_1'A'\), \(E'C_1'D_1'B'\) passing through \(F_1\) are inscribed too. Hence \[\angle A'B'C'=\angle C'D'E'=\angle E'A'B'=\angle B'C'D'=\angle D'E'A'.\] From these equalities and the fact that \(A'B'C'D'E'\) is inscribed we deduce that each four of its vertices form an isosceles trapezoid whence this pentagon is regular. This means that \(A_1'B_1'C_1'D_1'E_1'\) is regular too and that \(F\) is its center. Thus \(A', F', A_1'\) are collinear, or equivalently \(A, F, A_1, F_1\) are concyclic. Consequently the diagonals \(AA_1\) and \(FF_1\) are concurrent at a point \(P\). Similarly we get the concurrencies of the diagonal pairs \(AA_1, BB_1\) and \(FF_1, BB_1\). Since \(AA_1, BB_1, FF_1\) are not coplanar, \(BB_1\) passes through \(P\). Similarly all the other diagonals pass through \(P\).
Now let \(e\) and \(e_1\) be opposite edges of the dodecahedron. Let \(X, Y\) be the touch-points of \(\omega\) with the tangent planes through \(e\). Similarly define \(X_1, Y_1\).
Since the planes \(Xe, Ye, X_1e_1, Y_1, e_1\) are concurrent in the vertex \(S\) of the cone that touches \(\omega\) by the circle \(XYX_1Y_1\), the extensions of \(e\) and \(e_1\) pass through \(S\). Similarly \(P\) lies in the other planes joining opposite edges of the dodecahedron whence \(P\) lies on each of the diagonals.
Note. For any vertex of the considered dodecahedron its five adjacent vertices are coplanar. Indeed, denote each vertex by the triple of touch-points with the adjacent faces. Thus we need to prove that, for example the points \(ABD_1, BCE_1, CDA_1, DEB_1, EAC_1\) are coplanar, or equivalently that the homonym face-planes of \(\mathcal Q\) are concurrent (due to polar duality). Inverting with center \(F\) they become five spheres. We know that both \(A_1B_1C_1D_1E_1\) and \(ABCDE\) are regular pentagons with center \(F_1\). Assume hereafter that \(X\) is the image of \(X\). Let \(B_2\) be the second intersection point of the circles \(ABD_1\) and \(BCE_1\). Clearly \(B, B_2, F_1\) are collinear. Let \(X\) and \(Y\) be the second intersection points of \(F_1F\) with the spheres \(ABD_1F\) and \(BCE_1F\) respectively. We have \(F_1F\cdot F_1X=F_1B_2\cdot F_1B=F_1F\cdot F_1Y\) so \(X\equiv Y\). Similarly the other spheres too pass through \(X\equiv Y\).
Thanks to this property one can note that, for example the extensions of faces corresponding to \(F\) and \(F_1\), as well as the planes \(ABCDE\) and \(A_1B_1C_1D_1E_1\) share a common line (the polar line of \(FF_1\) wrt \(\omega\)).